TEORIAS E FILOSOFIAS DE GRACELI 239

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.

\left(\alpha _{0}mc^{2}+\sum _{{j=1}}^{3}\alpha _{j}p_{j}\,c\right)\psi ({\mathbf {x}},t)=i\hbar {\frac {\partial \psi }{\partial t}}({\mathbf {x}},t)

[EQUAÇÃO DE DIRAC].

\Delta U={\frac {3}{2}}nR(T_{f}-T_{i})

+ FUNÇÃO TÉRMICA.

N=N_{{o}}.e^{{-\lambda .t}}

+ FUNÇÃO DE RADIOATIVIDADE

T=e^{-2bL}

b={\sqrt {\frac {8\pi ^{2}m(Ub-E)}{h^{2}}}}

\Delta S=S_{2}-S_{1}=\int _{1}^{2}{\frac {\delta Q}{T}}

+ ENTROPIA REVERSÍVEL

\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}

FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA

E_{p}={\sqrt {{\frac {\hbar c^{5}}{G}}}}\approx

ENERGIA DE PLANCK

$V [R] [MA] = Δ e, M, Δ f, Δ E, Δ t, Δ i, Δ T, Δ C, Δ E, Δ A, Δ D, Δ M......$
ΤDCG
X
Δe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
x
sistema de dez dimensões de Graceli +
DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.
x
sistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia.
x
TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
X
T l   T l    E l      Fl        dfG l
N l   El             tf l
P l   Ml           tfefel
Ta l   Rl
         Ll
D

Em química, a lei de ação das massas é um modelo matemático que explica e prediz comportamentos de soluções em equilíbrio dinâmico. Pode ser descrito com dois aspectos: 1) o aspecto do equilíbrio, relacionado à composição de uma mistura em reação em equilíbrio e 2) o aspecto cinético relacionado à equações de taxas para reações elementares. Ambos os aspectos advém da pesquisa por Cato Maximilian Guldberg e Peter Waage (1864-1879) na qual constantes de equilíbrio foram derivadas pelo uso de dados cinéticos e a equação de taxa a qual eles tinham proposto. Guldberg e Waage também reconheceram que equilíbrio químico é um processo no qual taxas de reação de um sentido de reação e seu inverso devem ser iguais.

Tomada como uma afirmação sobre cinética, a lei estabelece que a taxa de uma reação elementar (uma reação que procede somente através de um estado de transição, que é uma etapa de mecanismo) é proporcional ao produto das concentrações das moléculas participantes. Em química moderna isto é derivado usando mecânica estatística.

Tomada como uma afirmação sobre equilíbrio, esta lei dá uma expressão para a constante de equilíbrio, uma grandeza caracterizando equilíbrio químico. Em química moderna isto é derivado usando termodinâmica de equilíbrio.

Visão contemporânea[editar | editar código-fonte]

As constantes de afinidade, k₊ e k_-, do artigo de 1879 podem agora ser reconhecidas como as constantes de taxas. A constante de equilíbrio, K, foi derivada por ajustar-se as taxas de reação de um sentido e seu inverso para serem iguais. Isto também significou que as afinidades químicas das reações de um sentido e seu inverso são iguais. A expressão resultante

K={\frac {[S]^{\sigma }[T]^{\tau }\dots }{[A]^{\alpha }[B]^{\beta }\dots }}\,

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

\left(\alpha _{0}mc^{2}+\sum _{{j=1}}^{3}\alpha _{j}p_{j}\,c\right)\psi ({\mathbf {x}},t)=i\hbar {\frac {\partial \psi }{\partial t}}({\mathbf {x}},t)

[EQUAÇÃO DE DIRAC].

\Delta U={\frac {3}{2}}nR(T_{f}-T_{i})

+ FUNÇÃO TÉRMICA.

N=N_{{o}}.e^{{-\lambda .t}}

+ FUNÇÃO DE RADIOATIVIDADE

T=e^{-2bL}

b={\sqrt {\frac {8\pi ^{2}m(Ub-E)}{h^{2}}}}

\Delta S=S_{2}-S_{1}=\int _{1}^{2}{\frac {\delta Q}{T}}

+ ENTROPIA REVERSÍVEL

\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}

FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA

E_{p}={\sqrt {{\frac {\hbar c^{5}}{G}}}}\approx

ENERGIA DE PLANCK

$V [R] [MA] = Δ e, M, Δ f, Δ E, Δ t, Δ i, Δ T, Δ C, Δ E, Δ A, Δ D, Δ M......$
ΤDCG
X
Δe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
x
sistema de dez dimensões de Graceli +
DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.
x
sistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia.
x
TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
X
T l   T l    E l      Fl        dfG l
N l   El             tf l
P l   Ml           tfefel
Ta l   Rl
         Ll
D

é correta ^[1] mesmo da moderna perspectiva, separada do uso de concentrações em vez de atividade (o conceito de atividade química foi desenvolvido por Josiah Willard Gibbs, nos anos 1870, mas não foi amplamente conhecido na Europa até os anos 1890s).

A derivação das expressões de taxa de reação não é mais considerada ser válida. Todavia, Guldberg e Waage estavam no caminho certo quando sugeriram que a força condutora tanto para a reação num sentido quanto no seu inverso é igual quando a mistura está em equilíbrio. O termo usado para esta força foi afinidade química. Hoje a expressão para a constante de equilíbrio é derivada por ajustar-se o potencial químico das reações num sentido e no seu inverso para serem iguais. A generalização da lei de ação das massas, em termos de afinidade, para equilíbrio de estequiometria arbitrária foi uma conjectura arrojada e correta.

A hipótese que a taxa de reação é proporcional às concentrações dos reagentes é, estritamente falando, somente verdade para reações elementares (reações com uma única etapa de mecanismo). Para reações não elementares é possível apenas uma aproximação aplicando sua expressão à etapa mais lenta da reação.

r_{f}=k_{f}[A][B]\,

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

\left(\alpha _{0}mc^{2}+\sum _{{j=1}}^{3}\alpha _{j}p_{j}\,c\right)\psi ({\mathbf {x}},t)=i\hbar {\frac {\partial \psi }{\partial t}}({\mathbf {x}},t)

[EQUAÇÃO DE DIRAC].

\Delta U={\frac {3}{2}}nR(T_{f}-T_{i})

+ FUNÇÃO TÉRMICA.

N=N_{{o}}.e^{{-\lambda .t}}

+ FUNÇÃO DE RADIOATIVIDADE

T=e^{-2bL}

b={\sqrt {\frac {8\pi ^{2}m(Ub-E)}{h^{2}}}}

\Delta S=S_{2}-S_{1}=\int _{1}^{2}{\frac {\delta Q}{T}}

+ ENTROPIA REVERSÍVEL

\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}

FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA

E_{p}={\sqrt {{\frac {\hbar c^{5}}{G}}}}\approx

ENERGIA DE PLANCK

$V [R] [MA] = Δ e, M, Δ f, Δ E, Δ t, Δ i, Δ T, Δ C, Δ E, Δ A, Δ D, Δ M......$
ΤDCG
X
Δe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
x
sistema de dez dimensões de Graceli +
DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.
x
sistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia.
x
TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
X
T l   T l    E l      Fl        dfG l
N l   El             tf l
P l   Ml           tfefel
Ta l   Rl
         Ll
D

É também aplicável a reações de segunda ordem que podem não ser reações relacionadas. Guldberg e Waage foram afortunados nestas reações tal como a formação de ésteres e hidrólises, nas quais originalmente basearam sua teoria, realmente seguindo esta expressão de taxa.

Em geral muitas reações ocorrem com a formação de intermediários reativos, e/ou através de caminhos de reação paralelos. Contudo, todas as reações podem ser representadas como uma série de reações elementares e, se o mecanismo é conhecido em detalhes, a taxa de reação para cada etapa individual é dada pela expressão

r_{f}

tanto que a taxa total pode ser derivada das etapas individuais. Quando isto é feito a constante de equilíbrio é obtida corretamente das equações de taxa para as taxas de reação num sentido e seu inverso.

Um equilíbrio químico é a situação em que a proporção entre os reagentes e produtos de uma reação química se mantém constante ao longo do tempo. Foi estudado pela primeira vez pelo químico francês Claude Louis Berthollet em seu livro Essai de statique chimique de 1803.^[1]

Teoricamente, toda a reação química ocorre nos dois sentidos: de reagentes se transformando em produtos e de produtos se transformando de volta em reagentes. Contudo, em certas reações, como a de combustão, praticamente 100% dos reagentes são convertidos em produtos, e não se observa ocorrer o contrário (ou pelo menos não em escala mensurável); tais reações são chamadas de irreversíveis. Há também uma série de reações nas quais logo que certa quantidade de produto(s) é formada, este(s) torna(m) a dar origem ao(s) reagente(s); essas reações possuem o nome de reversíveis. O conceito de equilíbrio químico restringe-se às reações reversíveis.

Apesar das concentrações do(s) reagente(s) e do(s) produto(s) serem constantes no equilíbrio químico de uma reação, os fenômenos direto e inverso do processo, que é reversível, continuam ocorrendo, ambos na mesma velocidade. Dessa forma, as reações direta e inversa se anulam, o que justifica o fato das concentrações do(s) produto(s) e do(s) reagente(s) serem constantes no equilíbrio químico, apesar da reação nunca ser interrompida.

Reversibilidade de reações químicas[editar | editar código-fonte]

Um exemplo de reação reversível é a da produção da amônia (NH₃) a partir do gás hidrogênio (H₂) e do gás nitrogênio (N₂) — que faz parte do Processo de Haber:

N_2(g) + 3H_2(g)

\rightleftharpoons

2NH_3(g)_X_{FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.}

Note-se que a seta dupla (

\rightleftharpoons

) significa que a reação ocorre nos dois sentidos, e que o subscrito (g) indica que a substância se encontra na fase gasosa.

Nesta reação, quando as moléculas de nitrogênio e as de hidrogênio colidem entre si, há uma certa chance da reação entre elas ocorrer, assim como quando moléculas de amônia colidem entre si há uma certa chance de elas se dissociarem e de se reorganizarem em H₂ e N₂.

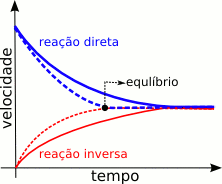
No início do processo, quando há apenas uma mistura de hidrogênio e nitrogênio, as chances das moléculas dos reagentes (H₂ e N₂) colidirem umas com as outras é a máxima de toda a reação, o que fará com que a taxa (ou velocidade) com que a reação ocorre também o seja. Porém à medida com que a reação se processa o número de moléculas de hidrogênio e de nitrogênio diminui, reduzindo dessa forma as chances de elas colidirem entre si e, consequentemente, a velocidade desse sentido da reação. Por outro lado, com o avançar da reação, o número de moléculas de amônia vai aumentando, o que faz com que cresçam as chances de elas colidirem e de se voltar a formar hidrogênio e nitrogênio, elevando assim a velocidade desse sentido da reação. Por fim chegará um momento em que tanto a velocidade de um dos sentidos quanto a do outro serão idênticas, nesse ponto nenhuma das velocidades variará mais (se forem mantidas as condições do sistema onde a reação se processa) e ter-se-á atingido o equilíbrio químico, conforme ilustrado nas figuras abaixo:

Velocidade das reações direta e inversa em função do tempo

Concentração das substâncias envolvidas em função do tempo

Um raciocínio similar, em princípio, pode ser aplicado para qualquer equilíbrio.

Deve-se salientar que quando uma reação atinge o equilíbrio ela não para. Ela continua se processando, porém tanto a reação direta como a inversa ocorrem à mesma velocidade, e desse jeito a proporção entre os reagentes e os produtos não varia . Por outras palavras, estamos na presença de um equilíbrio dinâmico (e não de um equilíbrio estático).

Constante de equilíbrio[editar | editar código-fonte]

Ver artigo principal: Constante de equilíbrio

"Por exemplo, a constante dessa reação na temperatura de 1000 K é 0,0413, note que a constante é ADIMENSIONAL*."

Referência: Atkins, Peter e Jones, Loretta - Princípios de Química 3º Edição
O equilíbrio químico é atingido quando, na mistura reacional, as velocidades das reações direta (reagentes formando produtos) e inversa (produtos formando regenerando os reagentes) ficam iguais.

Uma vez atingido o equilíbrio a proporção entre os reagentes e os produtos não é necessariamente de 1:1 (lê-se um para um). Essa proporção é descrita por meio de uma relação matemática, mostrada a seguir:

Dada a reação genérica:

\rightleftharpoons

onde A, B, Y e Z representam as espécies químicas envolvidas e a, b, y e z os seus respectivos coeficientes estequiométricos. A fórmula que descreve a proporção no equilíbrio entre as espécies envolvidas é:

K_{c}={\frac {[{\mbox{Y}}]^{{\mbox{y}}}\cdot [{\mbox{Z}}]^{{\mbox{z}}}}{[{\mbox{A}}]^{{\mbox{a}}}\cdot [{\mbox{B}}]^{{\mbox{b}}}}}

X

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

Os colchetes representam o valor da concentração (normalmente em mol/L) da espécie que está simbolizada dentro dele ([A] = concentração da espécie A, e assim por diante).

K_{c}

é uma grandeza chamada de constante de equilíbrio da reação. Cada reação de equilíbrio possui a sua constante, a qual sempre possui o mesmo valor para uma mesma temperatura. De um modo geral, a constante de equilíbrio de uma reação qualquer é calculada dividindo-se a multiplicação das concentrações dos produtos (cada uma elevada ao seu respectivo coeficiente estequiométrico) pela multiplicação das concentrações dos reagentes (cada uma elevada ao seu relativo coeficiente estequiométrico).

Um exemplo disso é a formação do trióxido de enxofre (SO₃) a partir do gás oxigênio (O₂) e do dióxido de enxofre (SO_2(g)) — uma etapa do processo de fabricação do ácido sulfúrico:

\rightleftharpoons

A constante de equilíbrio desta reação é dada por:

K_{c}={\frac {[{\mbox{SO}}_{{\mbox{3}}}]^{{\mbox{2}}}}{[{\mbox{SO}}_{{\mbox{2}}}]^{{\mbox{2}}}\cdot [{\mbox{O}}_{{\mbox{2}}}]}}

X

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

É possível determinar experimentalmente o valor da constante de equilíbrio para uma dada temperatura. Por exemplo, a constante dessa reação na temperatura de 1000 K é 0,0413. A partir dela, dada uma certa quantidade conhecida de produtos adicionados inicialmente em um sistema nessa temperatura, é possível calcular por meio da fórmula da constante qual será a concentração de todas as substâncias quando o equilíbrio for atingido. É importante notar que, Kc para uma equação química SÓ depende da temperatura, não é alterado por catalisador e mede a espontaneidade da reação direta, a partir da condição padrão ( 1 mol/l ou 1 atm )

Utilizando a relação:

\Delta G=\Delta H-T\Delta S

, onde ΔG é a energia livre de Gibbs, T a temperatura absoluta e ΔS e a variação da entropia.

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

Podemos colocá-la da seguinte forma:

(I)

G=H-TS

( É possível por ser função de estado )

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

E sabendo que:

(II)

H=U+PV

, onde U e a energia interna, P é a pressão e V o volume.

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

Derivando (I) temos:

dG=dH-d(TS)\rightarrow dG=d(U+PV)-TdS-SdT\rightarrow dG=dU+PdV+VdP-TdS-SdT

(III),

Sabendo que:

dS=dQ_{{rev}}/T\rightarrow dQ_{{rev}}=TdS

(IV)

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

Tendo que:

dU=dQ-PdV

(V)

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

Inserindo (IV) e (V) em (III)

dG=dU+PdV+VdP-TdS

, onde TdS = 0 pois,

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

Para P e T constantes temos:

dG=dQ-PdV+VdP-dQ

, onde PdV = 0

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

Integrando a equação de Gº ( G padrão ) a G e de Pº ( "P zero" = P padrão ) temos :

\int dG=\int VdP=G-G^{0}=\int (nRT/P)dP

, onde n é o nº de moles, R a constante universal dos gases.

G-G^{0}=RT\ln(P/P^{0})

X

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

Onde Pº = 1 atm, note que daqui fica extremamente claro que o K é adimensional, pois P/Pº é adimensional.

Chegamos:

G=G^{0}+RT\ln P

(VI) , onde ln P é o logaritmo de base e de P.

Agora tendo uma reação:

aA + bB

\rightarrow

cC + dD (reação direta)

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

cC + dD

\rightarrow

aA + bB (reação inversa)

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

\Delta G=Gp-Gr

, onde Gp é a energia dos produtos e Gr a energia dos reagentes.

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

Colocando (VI) nessa equação, conclui - se:

\Delta G=\Delta G^{0}+RT\ln[X/Y]

X

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

Onde X = A multiplicação das pressões parciais dos produtos elevado a seus respectivos coeficientes estequiométricos e Y idem para os reagentes.

X/Y=Q

, onde Q é o quociente da reação.

Para o equilíbrio temos que K = Q e ΔG = 0*

ΔG = 0 pois a reação direta e inversa não são espontâneas, portanto é possível afirmar que o equilíbrio foi atingido!

Temos por fim:

0=\Delta G^{0}+RT\ln K

, concluindo:

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

K=e^{{(-\Delta G^{0}/RT)}}

X

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

Note que aqui fica mais claro ainda que o K é adimensional e que o K de uma reação elementar é o mesmo, caso a reação não seja elementar, por causa da função de estado, onde ΔG_f = ΔG_i, logo K não depende do caminho percorrido, só dependendo a temperatura. Note também que K mede a espontaneidade a partir da condição padrão.

As leis de Guldberg-Waage e de Arrhenius[editar | editar código-fonte]

É possível relacionar a lei de Guldberg-Waage e a Lei de Arrhenius a essa última fórmula. Assim, pela Lei de Guldberg-Waage:

v1=k1[X1],v2=k2[X2]

Onde k1,2 são as constantes cinéticas das reações direta e inversa, respectivamente, bem como [X1] e [X2] são as concentrações dos reagentes

Logo, no equilíbrio, v₁ = v₂, onde v1 é Velocidade da reação direta e v2 da inversa:

k1[X1]=k2[X2]\Rightarrow k1/k2=[X2]/[X1]=K

X

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

E para Lei de Arrhenius temos:

K=e^{-\Delta G^{o}/RT}=e^{-(\Delta H^{o}-\Delta S^{o}T)/RT}=[e^{-Eap/RT}][e^{Sp/R}]/[e^{-Ear/RT}][e^{Sr/R}]=k1/k2

X

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

Onde:

H é a entalpia, S é a entropia e Ea_p,r são as energias de ativação dos produtos e dos reagentes respectivamente. Dessa forma:

k=Ae^{(-Ea/RT)},A=e^{(S/R)}

X

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

Constante para a soma de reações[editar | editar código-fonte]

Se uma reação química pode ser expressa pela soma de duas ou mais reações (ou etapas individuais), então a constante de equilíbrio da reação global será a multiplicação das constantes de cada uma das reações individuais.

2P_(g) + 3Cl_2(g) $\rightleftharpoons$ 2PCl_3(g)	$K'_{c}={\frac {[{\mbox{PCl}}_{{\mbox{3}}}]^{{\mbox{2}}}}{[{\mbox{P}}]^{{\mbox{2}}}\cdot [{\mbox{Cl}}_{{\mbox{2}}}]^{{\mbox{3}}}}}$
PCl_3(g) + Cl_2(g) $\rightleftharpoons$ PCl_5(g)	$K''_{c}={\frac {[{\mbox{PCl}}_{{\mbox{5}}}]}{[{\mbox{PCl}}_{{\mbox{3}}}]\cdot [{\mbox{Cl}}_{{\mbox{2}}}]}}$
2P_(g) + 5Cl_2(g) $\rightleftharpoons$ 2PCl_5(g)	$K_{c}={\frac {[{\mbox{PCl}}_{{\mbox{5}}}]^{{\mbox{2}}}}{[{\mbox{P}}]^{{\mbox{2}}}\cdot [{\mbox{Cl}}_{{\mbox{2}}}]^{{\mbox{5}}}}}$

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

Neste caso, a terceira reação é igual à soma da primeira mais duas vezes a segunda:

+	2P_(g) + 3Cl_2(g) $\rightleftharpoons$ 2PCl_3(g)
	PCl_3(g) + Cl_2(g) $\rightleftharpoons$ PCl_5(g)
	PCl_3(g) + Cl_2(g) $\rightleftharpoons$ PCl_5(g)
	2P_(g) + 5Cl_2(g) $\rightleftharpoons$ 2PCl_5(g)

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

E a sua constante de equilíbrio pode ser expressa por:

K_{c}=K'_{c}\cdot K''_{c}\cdot K''_{c}

K_{c}={\frac {[{\mbox{PCl}}_{{\mbox{3}}}]^{{\mbox{2}}}}{[{\mbox{P}}]^{{\mbox{2}}}\cdot [{\mbox{Cl}}_{{\mbox{2}}}]^{{\mbox{3}}}}}\cdot {\frac {[{\mbox{PCl}}_{{\mbox{5}}}]}{[{\mbox{PCl}}_{{\mbox{3}}}]\cdot [{\mbox{Cl}}_{{\mbox{2}}}]}}\cdot {\frac {[{\mbox{PCl}}_{{\mbox{5}}}]}{[{\mbox{PCl}}_{{\mbox{3}}}]\cdot [{\mbox{Cl}}_{{\mbox{2}}}]}}={\frac {[{\mbox{PCl}}_{{\mbox{5}}}]^{{\mbox{2}}}}{[{\mbox{P}}]^{{\mbox{2}}}\cdot [{\mbox{Cl}}_{{\mbox{2}}}]^{{\mbox{5}}}}}

X

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

Pode se perceber que caso uma reação apareça duas ou mais vezes na soma, ela aparece esse mesmo número de vezes na multiplicação.

Relação entre a velocidade da reação e a constante de equilíbrio[editar | editar código-fonte]

Conforme já mencionado, no equilíbrio a velocidade tanto da reação inversa quanto a da direta são iguais. Por sua vez, a velocidade de uma reação depende de uma outra constante chamada de constante de velocidade (simbolizada aqui por

k

); e é possível encontrar uma relação entre as constantes de velocidade das reações direta e indireta, e a constante de equilíbrio.

Para demonstrar isso, considere-se o seguinte equilíbrio genérico (supondo que as suas reações ocorram cada qual em uma única etapa):

\rightleftharpoons

X + Y

K_{c}={\frac {[{\mbox{X}}]\cdot [{\mbox{Y}}]}{[{\mbox{A}}]^{{\mbox{2}}}}}

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

Agora vejamos as duas reações que ocorrem nele, juntamente com a expressão de suas respectivas velocidades (

r

2A → X + Y	$r=k\cdot [{\mbox{A}}]^{{\mbox{2}}}$
X + Y → 2A	$r'=k'\cdot [{\mbox{X}}]\cdot [{\mbox{Y}}]$

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

É importante frisar que o expoente que eleva as concentrações das espécies na fórmula da velocidade não necessariamente é igual ao respectivo coeficiente estequiométrico da espécie na reação, contudo o expoente certamente será assim se a reação se processar em uma única etapa (conforme se está considerando nessa situação).

Uma vez que as velocidades de ambas as reações são idênticas no equilíbrio, pode-se igualá-las:

k\cdot [{\mbox{A}}]^{{\mbox{2}}}=k'\cdot [{\mbox{X}}]\cdot [{\mbox{Y}}]

X

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

Rearranjando a equação, tem-se:

{\frac {[{\mbox{X}}]\cdot [{\mbox{Y}}]}{[{\mbox{A}}]^{{\mbox{2}}}}}={\frac {k}{k'}}

X

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

Observemos que a expressão do membro esquerdo é idêntica à fórmula do equilíbrio dessa reação. Então podemos escrever:

K_{c}={\frac {k}{k'}}

X

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

Esta relação é válida para qualquer equilíbrio cujas reações ocorram em uma única etapa, o que pode ser facilmente constatado por essa mesma dedução para outros equilíbrios.

No caso de as reações se processarem em mais de uma etapa, basta lembrar que a reação global nada mais é que a soma das reações de cada etapa. Para cada uma das etapas pode-se fazer essa mesma dedução, e então somar cada reação (o que significa multiplicar as suas constantes). Dessa forma teremos para uma reação de múltiplas etapas:

K_{c}={\frac {k_{1}}{k'_{1}}}\cdot {\frac {k_{2}}{k'_{2}}}\cdot (\cdots )

X

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

Sendo

k_{1}

k'_{1}

k_{2}

k'_{2}

e assim por diante as constantes de velocidades de cada etapa.

Equilíbrio heterogêneo[editar | editar código-fonte]

Quando todas as substâncias envolvidas no equilíbrio se encontram no mesmo estado físico diz-se que temos um equilíbrio homogêneo, que é o caso de todos os equilíbrios apresentados aqui até então. Analogamente, os equilíbrios onde estão envolvidas mais de uma fase são chamados de equilíbrios heterogêneos, como o seguinte:

Ni_(s) + 4CO_(g)

\rightleftharpoons

Ni(CO)_4(g)

_{FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.}

Note-se que o subscrito (s) significa que a espécie se encontra no estado sólido. Equilíbrios heterogêneos, como este, frequentemente apresentam ao menos um sólido puro ou um líquido puro.

Na expressão da constante de equilíbrio temos as concentrações das espécies envolvidas. A concentração pode ser calculada dividindo-se o número de mols da substância pelo volume que ela ocupa. O número de mols representa a quantidade de matéria e, por isso, ele é proporcional a massa; assim o número de mols dividido pelo volume é proporcional à massa dividida pelo volume.

A densidade de algo é justamente calculada dividindo-se a sua massa pelo seu volume ocupado. No caso de uma substância pura, toda a sua massa corresponde à de uma única substância, e assim a sua "concentração" do seu número de mols dividido pelo volume é proporcional a sua densidade (massa dividida pelo volume).

A densidade de uma dada substância em dadas condições é uma propriedade intensiva, ou seja, é a mesma independentemente do quanto dessa substância houver. Dessa forma pode-se concluir que a concentração de um sólido ou um líquido puro (que são virtualmente incompressíveis) é a mesma independentemente de quanto houver deles (já um gás, que pode ser comprimido sem dificuldade, tem a sua concentração variada facilmente). Por essa razão se simplifica as expressões das constantes de equilíbrio omitindo-se a concentração de sólidos e líquidos puros.

Com isso, a expressão para a constante do último equilíbrio apresentado fica:

K_{c}={\frac {[{\mbox{Ni}}{\mbox{(CO)}}_{4}]}{[{\mbox{CO}}]^{{\mbox{4}}}}}

X

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

Equilíbrio gasoso[editar | editar código-fonte]

Pela equação dos gases perfeitos tem-se que para cada gás de uma mistura gasosa:

P_{x}\cdot V=n_{x}\cdot R\cdot T

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

onde

P_{x}

é a pressão parcial de um gás

x

qualquer (ou seja, a pressão que ele teria caso estivesse apenas ele no recipiente),

V

é o volume ocupado pela mistura,

n_{x}

é o número de mols do gás,

R

é a constante dos gases perfeitos, e

T

a temperatura em kelvin.

Rearranjando a equação, teremos:

{\frac {n_{x}}{V}}={\frac {P_{x}}{R\cdot T}}

X

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

O membro esquerdo (

n_{x}

V

) é a fórmula para o cálculo da concentração molar do gás. A constante

R

é sempre a mesma e a temperatura

T

não varia em um sistema que permanece em equilíbrio químico, assim o único fator que pode variar na equação em um equilíbrio é a pressão parcial

P_{x}

. Dessa forma pode-se dizer que a concentração do gás é proporcional à sua pressão parcial.

Com base nisso, também é possível escrever a fórmula da constante de equilíbrio usando-se as pressões parciais dos gases envolvidos, no lugar de suas concentrações. Por exemplo:

H_2(g) + I_2(g)

\rightleftharpoons

2HI_(g)

K_{p}={\frac {\left(P_{{HI}}\right)^{2}}{P_{{H_{2}}}\cdot P_{{I_{2}}}}}

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

Observe-se que agora a constante de equilíbrio está representada por

K_{p}

, em vez de

K_{c}

(quando o cálculo foi feito usando-se as concentrações dos gases). Essas duas constantes para um mesmo caso possuem valores diferentes uma da outra, então é importante especificar qual das duas se está usando quando se está lidando com um equilíbrio.

Adição ou remoção de reagentes (Não serve para sólidos)[editar | editar código-fonte]

Ao se alterar a quantidade de uma substância, também se está mexendo na velocidade em que a reação se processa (pois se estará mudando as chances de as substâncias reagirem entre si). Dessa forma, a velocidade das reações direta e inversa deixa de ser igual: se uma substância foi retirada de uma das reações, essa passará a ser mais lenta; e, analogamente, ela passará a ser mais rápida se uma substância for adicionada a ela. Assim ocorre que se algo for acrescentado, o equilíbrio tende a reduzir a quantidade dessa substância e vice-versa. Para garantir que a reação se torne reversa

Tal resposta do equilíbrio pode ser sumarizada pelo assim chamado Princípio de Le Chatelier:

Quando uma perturbação externa é aplicada a um sistema em equilíbrio dinâmico, o equilíbrio tende a se ajustar para diminuir o efeito da perturbação.

À medida que as reações se processam, as suas velocidades vão se aproximando até que se igualem e assim é atingido novamente o equilíbrio. A constante do equilíbrio será a mesma da de antes de se adicionar ou remover substâncias.

Compressão[editar | editar código-fonte]

Um equilíbrio gasoso pode ser afetado pela compressão. De acordo com o princípio de Le Chatelier, com o aumento da pressão o equilíbrio tende a se deslocar no sentido de diminuir essa pressão, o que significa favorecer a reação que resulte no menor número de moléculas no estado gasoso. Nesse caso, a o valor da constante de equilíbrio também não é alterado.

Para se observar tal efeito, considere-se esse equilíbrio:

N₂O_4(g)

\rightleftharpoons

2NO_2(g)

K_{c}={\frac {[{\mbox{NO}}_{{\mbox{2}}}]^{{\mbox{2}}}}{[{\mbox{N}}_{{\mbox{2}}}{\mbox{O}}_{{\mbox{4}}}]}}

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

As concentrações podem ser escritas como o seu número de mols dividido pelo volume (

n_{x}/V

), então teremos:

K_{c}={\frac {({n_{{NO_{2}}}}/V)^{2}}{({n_{{N_{2}O_{4}}}}/V)}}={\frac {(n_{{NO_{2}}})^{2}}{(n_{{N_{2}O_{4}}})}}\cdot {\frac {1}{V}}

X

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

Se o valor de

V

(volume) diminuir, é preciso que o número de mols do N₂O₄ aumente para que o valor da constante de equilíbrio permaneça o mesmo. Na reação, esse reagente representava metade do número de moléculas do produto. O mesmo raciocínio pode ser aplicado em qualquer equilíbrio gasoso.

Temperatura[editar | editar código-fonte]

É encontrado experimentalmente que a formação de produtos de uma reação exotérmica (isto é, que liberta energia) é favorecida com a diminuição da temperatura, ao passo que a formação de produtos em uma reação endotérmica (isto é, que absorve energia) é favorecida com o aumento da temperatura.

Em um equilíbrio, se uma reação é endotérmica a outra necessariamente é exotérmica, e vice-versa. Aumentar ou diminuir a temperatura fará com que a velocidade de uma das reações aumente e a da outra diminua. As velocidades das reações se igualarão novamente depois de um tempo; porém nesse caso como temos o favorecimento e o desfavorecimento da formação de certas substâncias, a constante de equilíbrio nessa nova temperatura não será mais a mesma da temperatura anterior.

Catalisador[editar | editar código-fonte]

A adição de um catalisador direciona a reação para um novo mecanismo, o qual é mais rápido do que o sem a catálise. Contudo, o catalisador não afeta o valor da constante de equilíbrio, ele apenas faz com que o equilíbrio seja atingido em um tempo menor, conforme mostrado na figura a seguir:

Curvas tracejadas: com catalisador Curvas cheias: sem catalisador

Atenção: O equilíbrio não é deslocado com a presença do catalisador.

Relação entre as constantes K_p e K_c[editar | editar código-fonte]

Existe uma relação matemática entre as constantes de equilíbrio em função da concentração K_c e em função da pressão parcial K_p, baseada na equação de Clapeyron:

K_{p}=K_{c}\left(RT\right)^{{\Delta n}}

X

FUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

em que: R é a constante universal dos gases, T é a temperatura absoluta e Δn é a diferença entre a soma dos coeficientes inteiros dos produtos gasosos e a soma dos coeficientes inteiros dos reagentes gasosos. Por exemplo, no equilíbrio:

aA_(g) + bB_(g) + cC_(s)

\rightleftharpoons

yY_(g) + zZ_(g)Δn = (y + z) - (a + b)XFUNÇÃO FUNDAMENTAL E GERAL DE GRACELI.

Essa expressão matemática apresenta uma limitação, não admitindo a presença de um ou mais líquidos na reação em questão. Isso não significa que a reação não apresente K_p e K_c, significa apenas que a expressão é inválida para esse caso.

quinta-feira, 12 de setembro de 2019

Miscibilidade é a capacidade de uma mistura formar uma única fase (mistura homogênea) em certos intervalos de temperatura, pressão e composição ^[1].

Mistura é o conjunto de duas ou mais substâncias puras. Quando duas substâncias são insolúveis, elas formam fases quando misturadas; o exemplo mais conhecido disto é a mistura óleo-água. Por outro lado, a água e o álcool etílico são solúveis em quaisquer proporções (miscíveis), enquanto que algumas outras combinações de substâncias são parcialmente solúveis; por exemplo, se colocarmos sal de cozinha em água além de uma certa quantia (acima da solubilidade), o excesso de sal adicionado não irá se solubilizar, descendo até o fundo da vasilha em sua forma sólida cristalina. Embora este exemplo seja de uma solução, mas que não deixa de ser um tipo de mistura, nesse caso, heterogênea, pois o excesso de sal não se dissolveu em água.

A solubilidade é em parte uma função da entropia e, por isso, é visto mais usualmente em estados da matéria que são mais entrópicos. Gases solubilizam-se quase que imediatamente, enquanto que sólidos raramente são solúveis por completo. Duas exceções úteis a esta regra são as soluções sólidas de cobre com níquel (o cuproníquel, usado em moedas e, especialmente, em encanamentos) e as de silício com germânio (usada em Eletrônica). Substâncias com entropia configuracional extremamente baixas, especialmente polímeros, dificilmente dissolvem-se entre si, mesmo no estado líquido. Isso quer dizer que não se pode jamais confundir "Misturar" com "Dissolver". Água e óleo se misturam (mistura heterogênea), mas não se dissolvem.

A solubilidade não depende apenas da entropia , pois se fosse verdade então a maioria das substâncias seriam solúveis , mas isso não ocorre na realidade e a solubilidade depende de outros fatores( temperatura , pressão , interação intermolecular ) . Nos compostos iónicos existem dois fatores antagónicos ( a energia da rede cristalina e a energia de hidratação . A energia da rede cristalina está relaciona com a disposição dos iões no estado sólido ( eles formam um retículo cristalino no qual as atracções são de natureza eletroestática e regidas pela lei de Coulomb , isto é ,diretamente proporcional ao produto das cargas dos iões e inversamente ao quadrado do raio iónico. A energia da rede cristalina "trabalha" contra a dissolução de um composto iónico, enquanto a energia de hidratação "trabalha" para favorecer a solubilidade do mesmo em água e está relaciona com a força ion-dipolo.

A energia de rede entre duas partículas é dada por ^[2]:

E_{el}=K{\frac {Q_{1}Q_{2}}{d}}

x

\left(\alpha _{0}mc^{2}+\sum _{{j=1}}^{3}\alpha _{j}p_{j}\,c\right)\psi ({\mathbf {x}},t)=i\hbar {\frac {\partial \psi }{\partial t}}({\mathbf {x}},t)

Sendo,

K

a constante

8,99X10^{2}Jm/C^{2}

Q_{1}

Q_{2}

são as cargas das partículas

d

a distância entre os centros das partículas

\left(\alpha _{0}mc^{2}+\sum _{{j=1}}^{3}\alpha _{j}p_{j}\,c\right)\psi ({\mathbf {x}},t)=i\hbar {\frac {\partial \psi }{\partial t}}({\mathbf {x}},t)

Valor de R	Unidades
287,0530 (ar)	J · kg⁻¹ . K⁻¹
8,3144621	J · K⁻¹ · mol⁻¹
0,0820574587	L · atm · K⁻¹ · mol⁻¹
8,20574587 x 10⁻⁵	m³ · atm · K⁻¹ · mol⁻¹
8,314462	cm³ · MPa · K⁻¹ · mol⁻¹
8,314462	L · kPa · K⁻¹ · mol⁻¹
8,314462	m³ · Pa · K⁻¹ · mol⁻¹
62,3637	L · mmHg · K⁻¹ · mol⁻¹
62,3637	L · Torr · K⁻¹ · mol⁻¹
83,14462	L · mbar · K⁻¹ · mol⁻¹
1,987	cal · K⁻¹ · mol⁻¹
6,132439833	lbf · ft · K⁻¹ · g · mol⁻¹
10,73	ft³ · psi · °R⁻¹ · lb-mol⁻¹
8,63 x 10⁻⁵	eV · K⁻¹ · atom⁻¹
0,7302	ft³·atm·°R⁻¹·lb-mol⁻¹
1,987	Btu · lb-mol⁻¹ · °R⁻¹

Pesquisar este blog

TEORIAS E FILOSOFIAS DE GRACELI 238